形式语言与自动机

上下文无关文法

设计上下文无关文法

1. {aⁿbⁿc^md^m|n≥1,m≥1}∩{aⁿb^mc^mdⁿ|n≥1,m≥1}

   S->AB|T T->aTd|aCd A->aAb|ab B->cBd|cd C->bCc|bc

2. {aⁿb^m|n,m≥0∧n≥m}

   S->A|B A->aA|aC B->Bb|Cb C->aCb|ε

3. {aⁿb^m|n≥0,m≥0,3n≥m≥2n}

   S->aSbb|aSbbb|ε

4. {w|w∈{a,b}^*,w中a和b的数目不同}

   S->A|B A->AA|Ta B->BB|Tb T->aTbT|bTaT|ε 注意此处T生成a与b数目相同的字符串

5. {w|w∈{a,b}^*,且w中a与b的数目相差为2}

   S->TaTaT|TbTbT T->aTbT|bTaT|ε

文法和语言中的二义性

文法无二义性：语法分析树唯一，亦等价于最左推导唯一

1. 下面的文法生成的是具有x和y的操作数、二元运算符+、-和*的前缀表达式：

   E->+EE|*EE|-EE|x|y

   证明这个文法是无歧义的。（Hopcroft, 5.4.7(b)）

   提纲：可证明其最左推导是唯一的，对字符串长度归纳，同时归纳证明生成的字符串w所有非空后缀字符串中操作数个数多于运算符个数。

有限自动机

安利一个用来画自动机的app：http://madebyevan.com/fsm/

设计DFA

1. 长度至少为2且头两个字符不相同的0,1串构成的集合

	0	1
->q0	q1	q2
q1	q4	q3
q2	q3	q4
*q3	q3	q3
q4	q4	q4

2. {w∈{a,b}^*|w中不包含子串aa}

	a	b
->*q0	q1	q0
*q1	q2	q0
q2	q2	q2

3. {w∈{a,b}^*|w中包含且仅包含奇数个子串ab}

	a	b
->q0	q1	q0
q1	q1	q2
*q2	q3	q2
q3	q3	q0

4. {w∈{a,b}^*|w中a的个数和b的个数之和是奇数}

	a	b
->q0	q1	q1
*q1	q0	q0

5. {w∈{a,b}^*|w含相同个数的a和b,且w的每个前缀中a和b个数之差不超过1}

	a	b
->*q0	q1	q2
q1	q3	q0
q2	q0	q3
q3	q3	q3

6. {w∈{a,b}^*|w包含子串ab，但不包含子串bb}

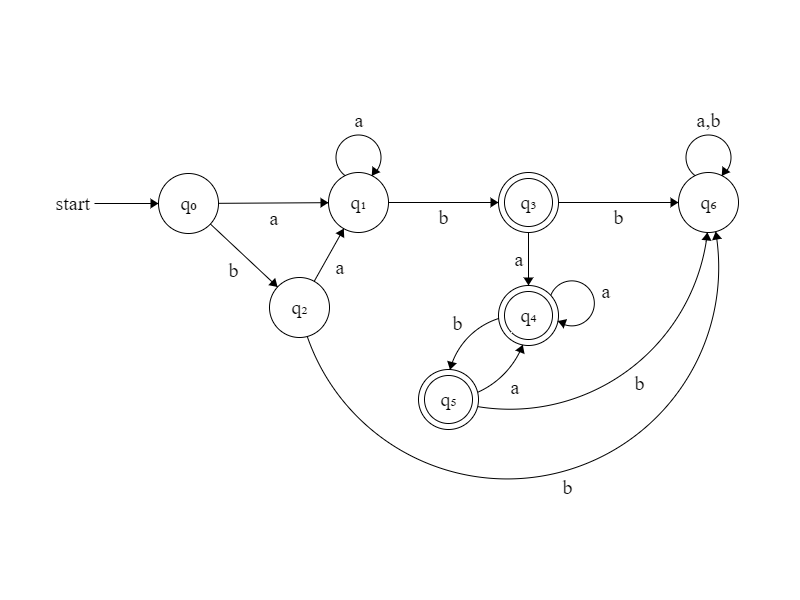
相应的NFA有：

此NFA遇到子串ab时到达终态，如果是最后一个ab，则停留在终态，反之跳转回q1。

DFA的最小化

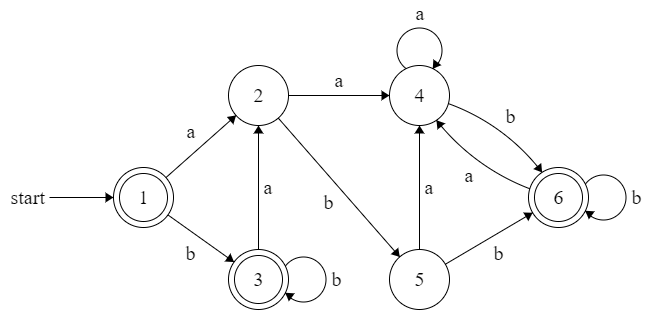
构造与该DFA等价的最小化的DFA：

填表算法第一步区分1，3，6与2，4，5

第二步区分2与4，5（输入字符b）

第三步区分1，3与6（输入字符a）

故最终等价类有{1, 3}, {2}, {4, 5}, {6}

最小化的DFA是

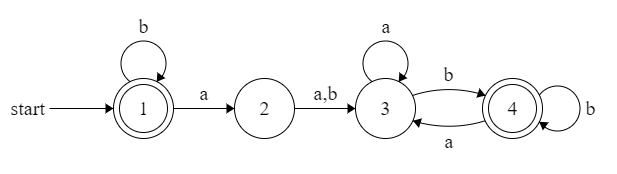
正规语言

设计正规语言

1. {xwx^R|x,w∈(a+b)+},其中(a+b)⁺=(a+b)(a+b)^*,x^R为x的反向(即反转)

   a(a+b)(a+b)^*a+b(a+b)(a+b)^*(a+b)

2. {w|w∈{a,b}^*∧∃x,y(x,y∈{a,b}^*∧w=xy∧|y|=3∧y=y^R)}

   (a+b)^*(aaa+aba+bab+bbb)

3. {w∈{a,b}^*|w中既不包含子串aa,也不包含子串bb}

   (ε+b)(ab)^*(ε+a)

4. {aⁿb^m|n,m≥0且n+m为偶数}

   (aa)^*(bb)^*+(aa)^*a(bb)^*b

5. {w|w∈{a,b}^*,|w|≥1,且w的后20位至少有一个a}

   (a+b)^*a(a+b+ε)¹⁹

6. {w|w∈{a,b}^*,|w|≥1,且当w以a结尾时,它的长度为奇数}

   ((a+b)(a+b))^*a+(a+b)^*b

7. {w|w∈{a,b}^*,|w|≥2,且w的前5位至少有一个子串aa}

   (a+b+ε)³aa(a+b)^*

8. {w|w∈{a,b}^*,|w|≥2,且w的第2位至第5位至少有一个a}

   (a+b)(a+b+ε)³a(a+b)^*

9. {w|w∈{0,1}^*,w至少含有3个1,且倒数第3位为1}

   (0+1)^*1(0+1)^*1(0+1)^*100+(0+1)^*1(0+1)^*1(01+10)+(0+1)^*111

有限状态自动机与正规表达式的关系

Thompson构造法

略

Kleene构造法&状态消去法

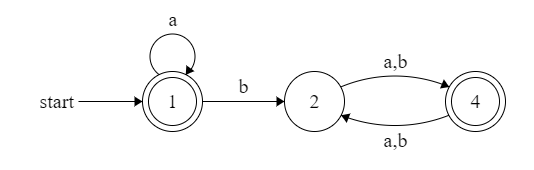
运用状态消去法，消2，1到4的弧变为b(a+b)，4到自身的弧变为(a+b)²

最终的正则表达式为a^*+a^*b(a+b)((a+b)²)^*

正规语言的性质

1. 语言L由所有满足如下条件的0，1串构成：0的数目二倍于1的数目。试应用Pumping引理证明L不是正规语言。

   对于任意n，取w=0²ⁿ1ⁿ，任意满足w=xyz∧|xy|≤n∧y≠ε的x，y，z必有y全由0组成，则xy⁰z中0比1的两倍少，不在L中，L不是正规语言。

2. 语言L由所有满足如下条件的0, 1串构成：0的数目多于1的数目（ 对0 和1 在串中出现的次序没有限制）。试应用Pumping引理证明L不是正规语言。

   选w=0ⁿ⁺¹1ⁿ